Basic concepts of reliability calculation of electronic assemblies

The reliability of electrical circuits is an important topic in medical technology, and it's becoming increasingly important. At least in my environment, the frequency of MTBF calculations is increasing, even though the validity of MTBF values is controversial. However, they can certainly be appropriate,

• to provide estimates of possible sources of error.
• when no test results are available yet, but figures are needed for reliability statements (for offers, estimates, etc.).
• to compare assemblies: similar complex assemblies should provide comparable values.

However, an MTBF value cannot replace testing. Testing is essential to obtaining a reliable product; more on this in a later blog post.

On the following pages, I have compiled some basic terms and links that I find helpful when dealing with MTBF calculations.

Terms

The reliability R (Reliability) is given by the following formula:  

• R is the reliability at time t.
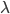•  is the Error rate, which indicates how many devices fail per unit of time. It is usually not constant (see below).

The MTBF is the Mean Time Between Failure, i.e. the average time until the next failure occurs.

The Error rate is with the MTBF connected by = 1 / MTBF and has the unit 1/h. So 1 error every 1000h means     = 10^-3 /h and MTBF = 1000h.

But be careful: The error rate is not a constant, but depends on time, temperature, voltage and other parameters! In the literature, the temporal dependence of the failure rate is usually seen following a "bathtub curve." According to EN61508, the failure rate is valid for 8–12 years. The failure rate and MTBF are not related by the simple inverse relationship for very long periods of time, since lambda is not constant in those cases. This is also clearly evident in human life expectancy [1]. Starting at the age of 50, the failure rate increases dramatically. If you calculate the MTBF using the failure rate of a 30-year-old, you get a life expectancy of 1300 years. :-)

The failure rate can change dramatically due to aging or fatigue. For example, electrolytic capacitors are specified for a certain service life under defined conditions. If this service life is exceeded or they are operated under different conditions, they do not fail suddenly, but they still leave the specified range, and subsequent failures (overvoltage, overheating) can occur.

One combined error rate  of several components, e.g. on a circuit board, is calculated using a simple sum:  

FIT (Failures In Time) describe the expected errors for an operating period of 10⁹ h, which corresponds to 114,000 years.

FIT and MTBF are connected by the formula: MTBF = 10⁹ h/FIT

MTTF Mean time to failure (MTF) is often equated with MTBF. MTTF is used for non-repairable failures, and MTBF for repairable failures.

The probability of failure F(t) results from the reliability with F(t) = 1 – R(t).

Important points

1. Due to the exponential function, 63.2% of the devices failed after the MTBF expired, i.e. when the devices were operated for the duration of the MTBF.
2. When aging occurs, the failure rate is not constant but increases with age. An MTBF value then provides no meaningful information.
3. The MTBF applies to a constant 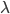, i.e., for the flat part of the bathtub curve. If you want to consider the change in the error rate over time, you have to work with Weibull distributions.
4. FIT values or error rates can be obtained from component manufacturers or from the following documents:

• Siemens SN29500
• MIL-HDBK 217 F
• Telcordia TR-332
• IEC62380
• FIDES Guide 2009 (UTE-C 80811)

These documents contain detailed formulas for determining failure rates depending on the environment, temperature, component type, housing, component complexity, etc. The operating conditions yield the so-called -values, which are multipliers for the standard failure rate that depend on the operating conditions. The above-mentioned documents contain detailed descriptions and formulas.

For calculating the failure rate at the PCB level, detailed instructions are provided in IEC62380 or in the FIDES Guide 2009 (UTE-C 80811). The FIDES Guide is available free of charge at http://www.fides-reliability.org/.

Documents worth reading

• Würth offers FIT values and instructions for calculating the probability of failure on its website for Würth components.

• In addition, there are various application notes from semiconductor manufacturers that can be found via Google.

• Several MIL standards address the topic of reliability and can be found free of charge online. Among them is MIL-STD-721, entitled "Definitions of Terms for Reliability and Maintainability." These can be found, for example, at: http://www.weibull.com/knowledge/milhdbk.htm

• A good introduction to MTBF calculation with simple examples can be found at: http://www.relnetyx.com/wp-content/uploads/2016/02/2012-MTBF-MTTF-RELNETyX-AG.pdf

Standards for reliability calculations

•  MIL-HDBK-217F; however, the last update dates back to 1995 and hasn't been maintained since then. However, as far as I know, the MIL standard is the basis for the other subsequent standards and is available free of charge. However, it contains very conservative assumptions, and the MTBF values calculated with it are correspondingly low.

• Telcordia SR-332 Reliability Prediction Procedure for Electronic Equipment is a further development of the MIL-HDBK-217F, after it was noticed that using the MIL-HDBK resulted in extremely pessimistic values. Telcordia has an interesting history; see the Wikipedia entry.

• NSWC Mechanical, The Handbook of Reliability Prediction Procedures for Mechanical Equipment (NSWC-07) from the Naval Surface Warfare Center, Carderock Division. This document dates from 2007 and contains models and data for mechanical components such as springs, pumps, valves, etc.

• The FIDES Guide 2009 (UTE-C 80811) dates from 2009 and was developed by French companies under the leadership of the DGA (Délégation Générale pour l'Armenent – French Ministry of Defense). It can be downloaded free of charge at http://www.fides-reliability.org/.

• IEC TR 62380 (formerly UTE C 80-810 RELIABILITY DATA HANDBOOK: RDF 2000) – This handbook specifies FIT rates for a wide variety of components. It also includes the derivation of the FIT values.

• DIN EN 61709 Electrical components – Reliability – Reference conditions for failure rates and stress models for conversion (IEC 61709:2011).

• IEC 62308:2006 Equipment reliability – Reliability assessment methods is more concerned with testing reliability and how to obtain reliable results and not so much with the theoretical models.

• Siemens Standard SN 29500-1: Component failure rates – expected values;
  It consists of several parts that describe different components.

• NSWC Standard 98/LE1 (Handbook of Reliability Prediction Procedures for Mechanical Equipment) is a standard for mechanical components published by the US Naval Surface Warfare Center and can be found on the Internet.

Final thoughts

Calculating reliability is an interesting and challenging task. Accordingly, there are experts and various tools that can assist you. The results of an MTBF calculation depend heavily on the standard used, and each source contains different theoretical models and values. Whenever possible, I would always use the manufacturer's values.

In our medical technology environment, a lot of testing is done to identify and correct potential weaknesses and errors during development. MTBF calculation is a practical tool for identifying and evaluating potentially error-prone circuit components.

Have fun calculating your MTBF! I welcome suggestions and exchanges of ideas.

Martin Bosch

[1] The example comes from a presentation on 61058, which is archived at the following link: https://web.archive.org/web/20110106035801/https://www.dke.de/de/Service/Nachrichten/documents/2aschenbrenner.pdf